O objectivo deste blog é partilhar
ideias e materiais com alunos, professores e outros eventuais
interessados. Ideias e materiais úteis para o estudo e para o ensino da
matemática .
Este blog foi criado com o
intuito de aprendermos juntos. O blog fala sobre conteúdos matemáticos,
explicações para o bom aprendizado do leitor. Estamos dispostos a ajudar
você que tem dificuldade a aprender e incorporar a matemática, com a
intenção de poder explicar e testar seus conhecimentos.
este blog é um trabalho escolar
do professor Renêe , foi criado por Mikael Castro , Wendy Rarunna , Risa
Raulino , Matheus Ferreira e Bárbara Mikaely .
domingo, 18 de dezembro de 2011
Vida e Obra de Pitágoras e Tales de Mileto

Pitágoras nasceu na ilha de Samos, no mar Egeu, e é provável que tenha viajado pela Ásia Menor e pelo Egito, como fizeram muitos filósofos gregos. Supõe-se também que tenha sido aluno de Tales. Há registro, porém, de que se mudou para o sul da Itália com cerca de 50 anos de idade. Na época, essa região era parte do mundo grego, e ali Pitágoras fundaria um núcleo de estudos.
Os ensinamentos veiculados nessa escola eram tidos pelos participantes como bastante preciosos e, por isso, os encontros de estudo eram mantidos em segredo. Supõe-se que abarcassem diversos aspectos do conhecimento, da filosofia à Matemática e Astronomia. É sensato crermos, também, que grande parte desses ensinamentos tenham se perdidos ou desvirtuado ao serem retransmitidos. O que se sabe é que as atividades do grupo geraram desconfianças, e Pitágoras precisou fugir da região na última década da sua vida.
No campo da Astronomia, Pitágoras foi o primeiro a afirmar, no mundo grego, que a Terra era esférica. Para ele, o sol, a Lua e os planetas apresentavam órbitas próprias. Isso lhe permitia concluir que esses astros não se situavam à mesma distância que as estrelas, mas que cada um deles estava situado numa camada esférica mais próxima. No centro dessas camadas concêntricas estaria a Terra.
À Pitágoras são ainda atribuídas várias descobertas sobre as propriedades dos números inteiros, a construção de figuras geométricas e a demonstração do teorema que leva seu nome (cujo enunciado já era conhecido pelos babilônios). Os próprios termos Filosofia (amor a sabedoria) e Matemática (o que é aprendido) seriam criações de Pitágoras para descrever suas atividades intelectuais.
Para alguns historiadores da matemática antiga, a geometria demonstrativa iniciou-se com Tales de Mileto, um dos sete sábios da Grécia. Foi o fundador da escola jônica, escola de pensamento dedicada à investigação da origem do universo e de outras questões filosóficas, entre elas a natureza e a validade das propriedades matemáticas dos números e das figuras.
Tales é uma figura imprecisa historicamente, pois não sobreviveu nenhuma obra sua.
O que sabemos é baseado em antigas referências gregas à história da matemática que atribuem à ele um bom número de descobertas matemáticas definidas.

Pouco sabemos sobre a vida e obra de Tales. Supõe-se que começou sua vida como mercador, tornando-se rico o suficiente para dedicar a parte final de sua vida ao estudo e a realização de algumas viagens. Supõe-se que viveu algum tempo no Egito onde provavelmente aprendeu geometria e na Babilônia onde entrou em contato com tabelas e instrumentos astronômicos.
Faz parte do seu mito o fato de ter previsto o eclipse solar de 585 a.C., embora muitos historiadores da ciência duvidem que os meios existentes na época permitissem tal proeza. Atribui-se a Tales o cálculo da altura das pirâmides, bem como o cálculo da distância até navios no mar, por triangulação.
Tales foi o primeiro personagem conhecido a quem associam-se descobertas matemáticas. Acredita-se que obteve seus resultados mediante alguns raciocínios lógicos e não apenas por intuição ou experimentação. Os fatos geométricos cuja descoberta é atribuída a Tales são:
A demonstração de que os ângulos da base de dois triângulos isósceles são iguais;
A demonstração do seguinte teorema: se dois triângulos tem dois ângulos e um lado respectivamente iguais, então são iguais;
A demonstração de que todo diâmetro divide um círculo em duas partes iguais;
A demonstração de que ao unir-se qualquer ponto de uma circunferência aos extremos de um diâmetro AB obtém-se um triângulo retângulo em C. Provavelmente, para demonstrar este teorema, Tales usou também o fato de que a soma dos ângulos de um triângulo é igual a dois retos;
Tales chamou a atenção de seus conterrâneos para o fato de que se duas retas se cortam, então os ângulos opostos pelo vértice são iguais.
Curiosidade .
QUEM INVENTOU A MATEMÁTICA?
 De acordo com o professor Odilon Otávio Luciano, do Instituto de Matemática da USP, não é possível atribuir a invenção da matemática a um único estudioso. "O que podemos dizer é que a tradição grega (de Pitágoras, Tales de Mileto e outros) deu início ao conceito matemático atual, que visa encontrar princípios simples capazes de explicar conceitos complexos", afirma. Mesmo assim, não se pode ignorar a influência que estes nomes receberam de outros indivíduos e culturas, como a egípcia.
De acordo com o professor Odilon Otávio Luciano, do Instituto de Matemática da USP, não é possível atribuir a invenção da matemática a um único estudioso. "O que podemos dizer é que a tradição grega (de Pitágoras, Tales de Mileto e outros) deu início ao conceito matemático atual, que visa encontrar princípios simples capazes de explicar conceitos complexos", afirma. Mesmo assim, não se pode ignorar a influência que estes nomes receberam de outros indivíduos e culturas, como a egípcia.Ângulos de um polígono convexo
A soma dos ângulos internos e externos de um polígno convexo .
Sabemos que a soma dos ângulos internos de um triângulo é igual a 180o.

Quadrilátero
Possui 4 LADOS
Pode ser dividido em 2 TRIÂNGULOS (a partir de um dos vértices)
Soma dos ângulos internos: 2 x 180o = 360o
Pentágono
Possui 5 LADOS
Pode ser dividido em 3 TRIÂNGULOS (a partir de um dos vértices)
Soma dos ângulos internos: 3 x 180o = 540o
Hexágono
Possui 6 LADOS
Pode ser dividido em 4 TRIÂNGULOS (a partir de um dos vértices)
Soma dos ângulos internos: 4 x 180o = 720o
Nos casos apresentados, qual a relação entre o número de lados do polígono e o número de triângulos encontrados em cada um, a partir de um dos vértices?
Se continuarmos desenhando polígonos e achando os triângulos possíveis a partir das diagonais de um dos vértices, perceberemos a mesma relação sempre.
E a soma dos ângulos internos desses polígonos sempre será:
(número de triângulos) x 180o
Pois, como vimos anteriormente, cada triângulo tem soma igual a 180o.
Como o número de triângulos é sempre o número de lados menos 2, se chamarmos o número de lados do polígono de n e a soma dos ângulos internos do mesmo de , podemos escrever a seguinte relação:
, podemos escrever a seguinte relação:
Exercícios resolvidos
1)Quanto vale a soma dos ângulos internos de um dodecágono?
n = 12
Sabemos que a soma dos ângulos internos de um triângulo é igual a 180o.
 |

Quadrilátero
 |
Possui 4 LADOS
Pode ser dividido em 2 TRIÂNGULOS (a partir de um dos vértices)
Soma dos ângulos internos: 2 x 180o = 360o
Pentágono
 |
Possui 5 LADOS
Pode ser dividido em 3 TRIÂNGULOS (a partir de um dos vértices)
Soma dos ângulos internos: 3 x 180o = 540o
Hexágono
 |
Possui 6 LADOS
Pode ser dividido em 4 TRIÂNGULOS (a partir de um dos vértices)
Soma dos ângulos internos: 4 x 180o = 720o
Nos casos apresentados, qual a relação entre o número de lados do polígono e o número de triângulos encontrados em cada um, a partir de um dos vértices?
Polígono
|
Número de lados
|
Número de triângulos
|
Relação
|
| Quadrilátero | 4 | 2 | 4 - 2 = 2 |
| Pentágono | 5 | 3 | 5 - 2 = 3 |
| Hexágono | 6 | 4 | 6 - 2 = 4 |
Se continuarmos desenhando polígonos e achando os triângulos possíveis a partir das diagonais de um dos vértices, perceberemos a mesma relação sempre.
E a soma dos ângulos internos desses polígonos sempre será:
(número de triângulos) x 180o
Pois, como vimos anteriormente, cada triângulo tem soma igual a 180o.
Como o número de triângulos é sempre o número de lados menos 2, se chamarmos o número de lados do polígono de n e a soma dos ângulos internos do mesmo de
 , podemos escrever a seguinte relação:
, podemos escrever a seguinte relação:  |
Exercícios resolvidos
1)Quanto vale a soma dos ângulos internos de um dodecágono?
n = 12
Diagonais de um polígono
Diagonais de um polígono .
Uma diagonal de um polígono é um segmento de reta entre dois vértices não consecutivos do polígono.
A fórmula para se calcular a quantidade de diagonais "P" que tem em um polígono de "n" lados é a seguinte:
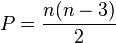
É necessário realçar que o triângulo não possui diagonais, e o pentágono é o único polígono, cujo número de diagonais é o mesmo que o número de lados.
Formula de caucular um polígono .
Tendo o retângulo acima como base para o estudo da fórmula, isolamos (limitamos nossa atenção) a um dos vértices, tomemos, por exemplo, o vértice A. Para esse vértice, somente é possível fazer diagonal com outro vértice não adjacente a ele, nesse caso, o vértice C. Os vértices B e D devem ser desconsiderados pois formam com o A dois dos lados do polígono.
Criamos uma fórmula que descreva a afirmação anterior:
Seja P o número de diagonais possíveis ao vértice A, desconsiderando os 3 (três) vértices com os quais não é possível ligar uma diagonal, a saber: B, D e o próprio A.
P = n − 3
Onde 'n' é o número de vértices do polígono.
Aplicando essa fórmula ao retângulo acima, temos: P = 4 − 3 portanto, para o vértice A uma só diagonal.
Se temos uma fórmula que calcula o número de diagonais para um vértice do polígono, bastaria então multiplicar essa fórmula pelo número de vértices desse polígono para aplicá-la aos outros vértices, porém, o que se observa é que o resultado será sempre o dobro do número de diagonais do polígono, veja:
P = n(n − 3)
P = 4(4 − 3) = 4
Isso se deve ao fato que uma diagonal é sempre "compartilhada" por dois vértices, daí a necessidade de se dividir por 2. Então:
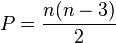
ou ainda:

Fica fácil agora entender matematicamente o porquê do triângulo não ter diagonais, uma vez que serão desconsiderados sempre 3 vértices: o próprio e os dois adjacentes.
Combinatoriamente, também é possível calcular o número de diagonais mediante o seguinte raciocínio:
Para cada par de pontos, existe um segmento de reta que os contém. Assim, a combinação de n vértices dois a dois fornece o número de segmentos possíveis entre dois vértices do polígono - há de se retirar, obviamente, o número de lados do polígono, pois estes também são segmentos possíveis entre dois vértices. Assim, temos:

Uma diagonal de um polígono é um segmento de reta entre dois vértices não consecutivos do polígono.
A fórmula para se calcular a quantidade de diagonais "P" que tem em um polígono de "n" lados é a seguinte:
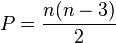
É necessário realçar que o triângulo não possui diagonais, e o pentágono é o único polígono, cujo número de diagonais é o mesmo que o número de lados.
Formula de caucular um polígono .
Tendo o retângulo acima como base para o estudo da fórmula, isolamos (limitamos nossa atenção) a um dos vértices, tomemos, por exemplo, o vértice A. Para esse vértice, somente é possível fazer diagonal com outro vértice não adjacente a ele, nesse caso, o vértice C. Os vértices B e D devem ser desconsiderados pois formam com o A dois dos lados do polígono.
Criamos uma fórmula que descreva a afirmação anterior:
Seja P o número de diagonais possíveis ao vértice A, desconsiderando os 3 (três) vértices com os quais não é possível ligar uma diagonal, a saber: B, D e o próprio A.
P = n − 3
Onde 'n' é o número de vértices do polígono.
Aplicando essa fórmula ao retângulo acima, temos: P = 4 − 3 portanto, para o vértice A uma só diagonal.
Se temos uma fórmula que calcula o número de diagonais para um vértice do polígono, bastaria então multiplicar essa fórmula pelo número de vértices desse polígono para aplicá-la aos outros vértices, porém, o que se observa é que o resultado será sempre o dobro do número de diagonais do polígono, veja:
P = n(n − 3)
P = 4(4 − 3) = 4
Isso se deve ao fato que uma diagonal é sempre "compartilhada" por dois vértices, daí a necessidade de se dividir por 2. Então:
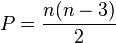
ou ainda:

Fica fácil agora entender matematicamente o porquê do triângulo não ter diagonais, uma vez que serão desconsiderados sempre 3 vértices: o próprio e os dois adjacentes.
Combinatoriamente, também é possível calcular o número de diagonais mediante o seguinte raciocínio:
Para cada par de pontos, existe um segmento de reta que os contém. Assim, a combinação de n vértices dois a dois fornece o número de segmentos possíveis entre dois vértices do polígono - há de se retirar, obviamente, o número de lados do polígono, pois estes também são segmentos possíveis entre dois vértices. Assim, temos:

|
|
|
|
|
sexta-feira, 16 de dezembro de 2011
História da Matemática .
A história da matemática é uma área de estudo dedicada, principalmente, à investigação sobre a origem das descobertas da matemática e, em uma menor extensão, à investigação dos métodos matemáticos e aos registros ou notações matemáticas do passado.
Matemática é uma ciência que foi criada a fim de contar e resolver problemas cujas existências tinham finalidades práticas. Teorias das mais complexas contadas por matemáticos sobrevoaram a mente humana de como a matemática foi criada.
Matemática é uma ciência que foi criada a fim de contar e resolver problemas cujas existências tinham finalidades práticas. Teorias das mais complexas contadas por matemáticos sobrevoaram a mente humana de como a matemática foi criada.
O que é geometria ?
Geometria .
A geometria é a parte da matemática cujo objeto de estudo é o espaço e as figuras que podem ocupá-lo. A partir da experiência, ou, eventualmente, intuitivamente, as pessoas caracterizam o espaço por certas qualidades fundamentais, que são denominadas axiomas de geometria (como, por exemplo, os axiomas de Hilbert ) . Esses axiomas não são provados, mas podem ser usados em conjunto com os conceitos matemáticos de ponto, linha reta, linha curva, superfíceis e sólido e para chegar a conclusões lógicas, chamadas de teorema.
Introdução .
Em Geometria, são conceitos intuitivos: o pnto, a reta e o plano.
O ponto não possui dimensões. Para representá-lo, basta fazer uma marca de papel. A sua indicação é feita,
A geometria é a parte da matemática cujo objeto de estudo é o espaço e as figuras que podem ocupá-lo. A partir da experiência, ou, eventualmente, intuitivamente, as pessoas caracterizam o espaço por certas qualidades fundamentais, que são denominadas axiomas de geometria (como, por exemplo, os axiomas de Hilbert ) . Esses axiomas não são provados, mas podem ser usados em conjunto com os conceitos matemáticos de ponto, linha reta, linha curva, superfíceis e sólido e para chegar a conclusões lógicas, chamadas de teorema.
Introdução .
Em Geometria, são conceitos intuitivos: o pnto, a reta e o plano.
O ponto não possui dimensões. Para representá-lo, basta fazer uma marca de papel. A sua indicação é feita,
Ângulos .
Ângulos .
Ângulo é a região de um plano concebida pela abertura de duas semi-retas que possuem uma origem em comum, chamada vértice do ângulo. A abertura do ângulo é uma propriedade invariante e é medida em radianos ou graus.
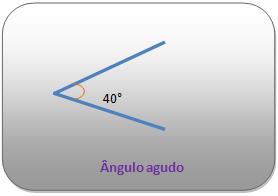
Ângulo agudo
O ângulo se torna agudo quando sua medida é menor que a medida de um ângulo reto de 90°.
Vejamos:
Ângulo obtuso
O ângulo se torna obtuso quando sua medida é maior que a medida de um ângulo reto de 90°.
Vejamos:
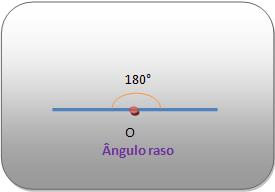
Ângulo raso
O ângulo se torna raso quando seus lados são semi – retas opostas e a medida for de dois retos de 180°.
Vejamos:
Ângulo é a região de um plano concebida pela abertura de duas semi-retas que possuem uma origem em comum, chamada vértice do ângulo. A abertura do ângulo é uma propriedade invariante e é medida em radianos ou graus.
Ângulo agudo
O ângulo se torna agudo quando sua medida é menor que a medida de um ângulo reto de 90°.
Vejamos:

Ângulo obtuso
O ângulo se torna obtuso quando sua medida é maior que a medida de um ângulo reto de 90°.
Vejamos:

Ângulo raso
O ângulo se torna raso quando seus lados são semi – retas opostas e a medida for de dois retos de 180°.
Vejamos:

Componentes de um ângulo
- Semi-retas - são os lados do ângulo.
- Origem ou vértice - ponto onde as duas semi-retas se encontram.
- Bissetriz - é a semi-reta com origem no vértice desse ângulo dividindo-o ao meio.
- Nulo: Um ângulo nulo mede 0°
- Agudo: Ângulo cuja medida é maior do que 0° e menor do que 90°
- Reto: Um ângulo reto é um ângulo cuja medida é exatamente 90°. Assim os seus lados estão localizados em retas perpendiculares.
- Obtuso: É um ângulo cuja medida está entre 90° e 180°.
- Raso: Ângulo que mede exatamente 180°, os seus lados são semi-retas opostas.
- Côncavo ou Reentrante: Ângulo que mede mais de 180°e menos de 360°.
- Giro ou Completo: Ângulo que mede 360°. Também pode ser chamado de Ângulo de uma volta.
Polígono .
Polígono .
Na geometria, um polígono é uma figura plana limitada por uma linha poligonal fechada: por exemplo, o hexágono é um polígono de seis lados.
A palavra "polígono" advém do grego e quer dizer muitos (poly) e ângulos (gon).
A definição usada por Euclides para polígono era uma figura limitada por linhas retas, sendo que estas linhas deveriam ser mais de quatro, e figura qualquer região do plano cercada por uma ou mais bordas.
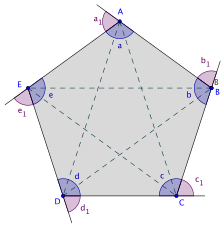
O Polígono e seus elementos .
Um polígono possui os seguintes elementos:
Na geometria, um polígono é uma figura plana limitada por uma linha poligonal fechada: por exemplo, o hexágono é um polígono de seis lados.
A palavra "polígono" advém do grego e quer dizer muitos (poly) e ângulos (gon).
A definição usada por Euclides para polígono era uma figura limitada por linhas retas, sendo que estas linhas deveriam ser mais de quatro, e figura qualquer região do plano cercada por uma ou mais bordas.
O Polígono e seus elementos .
Um polígono possui os seguintes elementos:
- Lados
- Cada um dos segmentos de reta que une vértices consecutivos:
 ,
,  ,
, ,
, ,
, .
.
- Vértices
- Ponto de encontro dos segmentos:
- A, B, C, D, E.
- Diagonais
- Segmentos que unem dois vértices não consecutivos:
 ,
, ,
, ,
, ,
, .
.
- Ângulos internos
- Ângulos formados por dois lados consecutivos:
 ,
, ,
, ,
, ,
,
- Ângulos externos
- Ângulos formados por um lado e pelo prolongamento do lado a ele consecutivo:
-
 ,
, ,
, ,
, ,
, .
.
Expressão Algébrica ou Literais .
Expressão Algébrica ou Literais .
Expressão é uma forma de demonstrar a resolução de um problema matemático onde envolve uma ou mais operações, por exemplo:
2 + 5 . (5 + 2)
- (-5) . 10 – (8 – 5)
5a + 5b + 10
Todos os exemplos acima são expressões, sendo que uma delas possui letras, esse tipo de expressão é chamado de expressões algébricas.
Expressões algébricas são expressões que possuem letras e número.
Valor numérico
Em uma expressão numérica é simples encontrar o seu valor numérico, pois basta resolve-la, veja um exemplo:
{5 . (-5 + 2)} – 2 =
{5 . (-3)} – 2 =
- 15 – 2 =
-17 VALOR NUMÉRICO.
Toda expressão algébrica tem o seu valor numérico, esse valor é encontrado a partir do momento em que temos ou atribuímos valores para as letras. Se em um exercício é pedido para que calcule o valor numérico da expressão algébrica 2x2y é preciso que saibamos ou atribuímos valores para as letras x e y.
Então vamos supor que na equação 2x2y, os valores das letras seja x = -2 e y = 1, agora substituindo esses valores, chegaremos em um valor numérico.
2x2y
2 . (-2)2 . 1
2 . 4 . 1
8 VALOR NUMÉRICO DA EXPRESSÃO 2x2y
Veja mais um exemplo de como achar o valor numérico da expressão a + ab + 5. O valor numérico desse e de todas as expressões algébricas irão variar dependendo do valor que iremos atribuir para as letras.
Nesse exemplo vamos supor que as letras a = 5 e b = -5.
5 + 5 . (-5) + 5
5 – 25 + 5
-20 + 5
-15 VALOR NUMÉRICO DA EXPRESSÃO a + ab + 5
Fator comum
As expressões algébricas são formadas por um ou mais termos, esses são chamados de monômios. Algumas expressões algébricas possuem termos (monômios) semelhantes. Quando isso acontece é preciso que una (opere) esses monômios semelhantes.
Para unir esses monômios é preciso que saiba que monômios semelhantes são aqueles que as partes literais são idênticas, ou seja, base (letras) e expoente idênticos. Veja um exemplo de monômios semelhantes:
5ab3 é semelhante de ab3, pois a parte literal das duas são idênticas.
Dada a expressão 18x2 + 5x – 4x2 + 6x para unir os termos semelhantes é preciso identificá-los, veja como:
18x2 – 4x2 + 5x + 6x
14x2 + 11x Essa expressão é a mesma que 18x2 – 4x2 + 5x + 6x só que com os termos semelhantes unidos é operado.
Expressão é uma forma de demonstrar a resolução de um problema matemático onde envolve uma ou mais operações, por exemplo:
2 + 5 . (5 + 2)
- (-5) . 10 – (8 – 5)
5a + 5b + 10
Todos os exemplos acima são expressões, sendo que uma delas possui letras, esse tipo de expressão é chamado de expressões algébricas.
Expressões algébricas são expressões que possuem letras e número.
Valor numérico
Em uma expressão numérica é simples encontrar o seu valor numérico, pois basta resolve-la, veja um exemplo:
{5 . (-5 + 2)} – 2 =
{5 . (-3)} – 2 =
- 15 – 2 =
-17 VALOR NUMÉRICO.
Toda expressão algébrica tem o seu valor numérico, esse valor é encontrado a partir do momento em que temos ou atribuímos valores para as letras. Se em um exercício é pedido para que calcule o valor numérico da expressão algébrica 2x2y é preciso que saibamos ou atribuímos valores para as letras x e y.
Então vamos supor que na equação 2x2y, os valores das letras seja x = -2 e y = 1, agora substituindo esses valores, chegaremos em um valor numérico.
2x2y
2 . (-2)2 . 1
2 . 4 . 1
8 VALOR NUMÉRICO DA EXPRESSÃO 2x2y
Veja mais um exemplo de como achar o valor numérico da expressão a + ab + 5. O valor numérico desse e de todas as expressões algébricas irão variar dependendo do valor que iremos atribuir para as letras.
Nesse exemplo vamos supor que as letras a = 5 e b = -5.
5 + 5 . (-5) + 5
5 – 25 + 5
-20 + 5
-15 VALOR NUMÉRICO DA EXPRESSÃO a + ab + 5
Fator comum
As expressões algébricas são formadas por um ou mais termos, esses são chamados de monômios. Algumas expressões algébricas possuem termos (monômios) semelhantes. Quando isso acontece é preciso que una (opere) esses monômios semelhantes.
Para unir esses monômios é preciso que saiba que monômios semelhantes são aqueles que as partes literais são idênticas, ou seja, base (letras) e expoente idênticos. Veja um exemplo de monômios semelhantes:
5ab3 é semelhante de ab3, pois a parte literal das duas são idênticas.
Dada a expressão 18x2 + 5x – 4x2 + 6x para unir os termos semelhantes é preciso identificá-los, veja como:
18x2 – 4x2 + 5x + 6x
14x2 + 11x Essa expressão é a mesma que 18x2 – 4x2 + 5x + 6x só que com os termos semelhantes unidos é operado.
quinta-feira, 15 de dezembro de 2011
Raiz Quadrada .
Raiz quadrada exata de um número racional .
Matematicamente, uma raiz quadrada de um número x é um número que, quando multiplicado por si próprio, iguala x. A raiz quadrada positiva de um número real não negativo x é simbolizada por √x. Por exemplo: porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadráticas (equações do 2º grau). A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos.
porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadráticas (equações do 2º grau). A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos.
Números quadrados perfeitos .
Os números que são quadrados de outros números denominam-se números quadrados perfeitos .
Matematicamente, uma raiz quadrada de um número x é um número que, quando multiplicado por si próprio, iguala x. A raiz quadrada positiva de um número real não negativo x é simbolizada por √x. Por exemplo:
 porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadráticas (equações do 2º grau). A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos.
porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadráticas (equações do 2º grau). A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos.Números quadrados perfeitos .
Os números que são quadrados de outros números denominam-se números quadrados perfeitos .
São quadrados perfeitos.
Veja tabela :
|
n
|
Raiz
|
|
0
|
0
|
|
1
|
1
|
|
4
|
2
|
|
9
|
3
|
|
16
|
4
|
|
25
|
5
|
|
36
|
6
|
|
49
|
7
|
|
64
|
8
|
|
81
|
9
|
|
100
|
10
|
|
121
|
11
|
|
144
|
12
|
|
169
|
13
|
|
196
|
14
|
|
225
|
15
|
|
n
|
Raiz
|
|
256
|
16
|
|
289
|
17
|
|
324
|
18
|
|
361
|
19
|
|
400
|
20
|
|
441
|
21
|
|
484
|
22
|
|
529
|
23
|
|
576
|
24
|
|
625
|
25
|
|
676
|
26
|
|
729
|
27
|
|
784
|
28
|
|
841
|
29
|
|
900
|
30
|
Assinar:
Postagens (Atom)